Intro

In the previous blog post on logits processing, we learned how we can influence the output generated by LLM based systems. If you are new to the topic, reading that article could give you a good introduction. However, here is the brief summary:

Logits Processing

LLMs work on the token level. Token can be considered as a small unit carrying meaning, like the syllable un or the word aircraft. LLMs have a vocabulary of tokens which are represented by their token ID, for instance the token fun could correspond to the token ID 7312.

For models published on huggingface, you typically find a file vocab.json or tokenizer.json which contains all tokens. For example, here is the tokenizer.json for smolLM2.

In the generation loop, LLMs receive a sequence of token IDs representing the text that has been generated so far. They then calculate a logit for each of the token IDs in their vocabulary. The logit represents the confidence of the LLM, that the associated token should be the next token in the sequence. This process is called prediction.

Usually, we follow the calculations of the LLM and select for instance the token with the largest logit to be next in the sequence. This is called sampling. Once the next token is selected, we pass the sequence with the chosen token prepended back to the LLM for another round in the generation loop.

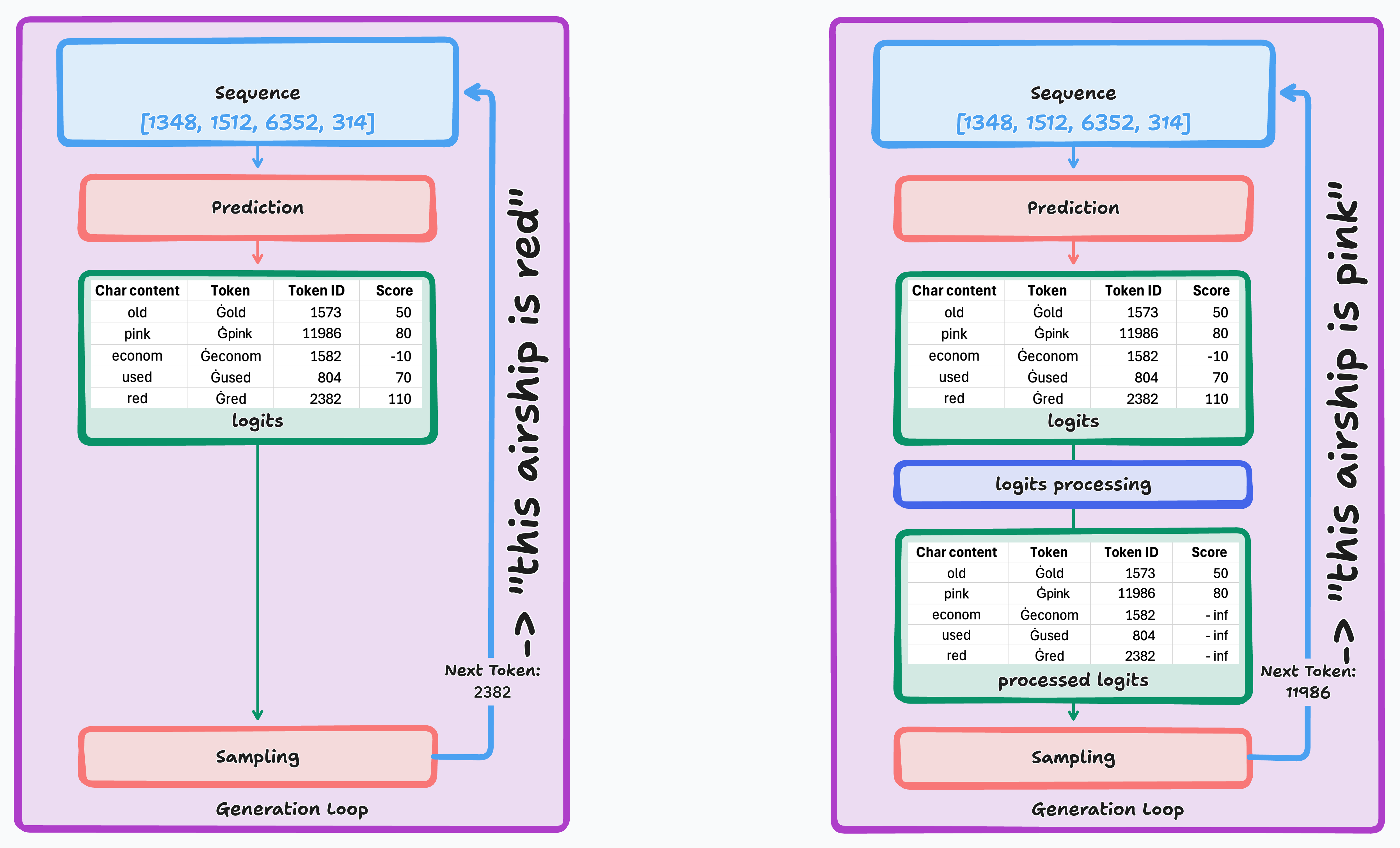
We can, however, hook into the process and transform the logits before selecting the next token. We've also seen how we can implement this in Bumblebee using logits processors. This process is called logit processing. More specifically, as we constrain the sampling step, we are talking about constrained sampling.

As an example, in our last blogpost we used Bumblebee's suppressed_tokens_processor to suppress the letter e:

We:

You are an AI Shakespeare writing poems. You are not allowed to use the letter e. Kindoms will fall if you do. Do NOT use the letter e. If you use the letter e it will have catastrophic consequences!

SmolLM2:

In cogs ach for task, in loops of data,
Through functionals, a pathway of data’s sway.
Functions of functionals, through loop's loop and spin,
Through functions of functional functions,
a pathway of function's win.

While the output will not win prices, it avoided the letter e, even with one one of the tiniest models out there! This is surprisingly easy and powerful. Can we use this to force LLM to comply to a grammar we specify?

Why bother?

When integrating LLM generated output in systems, we usually want the output to follow a schema we define. Some form of validation ensures that malformed LLM output is caught. We retry the generation, and hope for a better result.

This is often fine, as the non-deterministic behaviour of LLM often ensure that the next try will yield better results. However, this means a higher latency and sometimes not getting a result at all.

While larger LLM get outputs in JSON often correct, smaller model struggle with the complexity those grammars can bring.

This is comes as no surprise: Formatting data according to a schema is a task that is easy in non-ai programming, but when we look at the way tokens are created in LLM, it becomes clear why this mechanism is a bad choice for this kind of task.

Sadly, we can not just create an EBNF or JSON Schema representation of the format we want. This would mean to implement a parser for those formats with the reduced instruction set defn provides. Doable, but maybe not fun.

Modeling schemas as DFA

To enable more advanced structures, we first need some sort of representation of those as data, in fact we can model many schemas as Deterministic Finite Automaton (DFA).

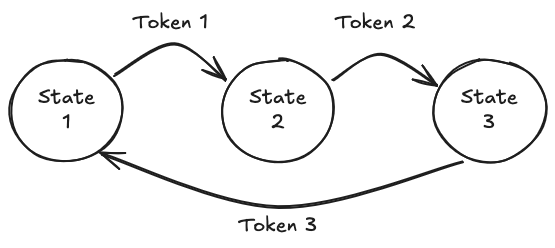
If we want to allow as output only the numbers 1, 2, 3 in exact this order (for instance 123, 123123, ...), we can model this as DFA.

Fundamentally, we need the following pieces of information for our DFA.

We need states, so we assign each number a state and get State 1, State 2, and State 3.

We must know which tokens are allowed in which state. In Elixir, we could model this as a map.

%{
  # state => allowed tokens
  1 => [1],
  2 => [2],
  3 => [3]
}

We must know to which state we move after we selected a token.

When we are in State 1, we can pick token 1 and move to State 2.
When we are in State 2, we can pick token 2 and move to State 3.
When we are in State 3, we can pick token 3 and move back to State 1.

In Elixir, we can represent these state transitions as list of tuples.

[
  # {state, token, next_state}
  {1, 1, 2},
  {2, 2, 3},
  {3, 3, 1}
]

In practice, we can derive the allowed tokens from the list of state transitions, squint your eyes and you'll see that for every state in the first column all allowed tokens are present in the second column.

So we can collapse these two data structures into the list of tuples that represent state transitions.

Last, we need the initial state. We want to allow 123 but not 3123, so we must start in State 1, the state in which the only allowed token is 1.

Stateful logits processors in Bumblebee

We've seen how logits processors work in Bumblebee and how to model advanced schemas as DFA. As a careful reader, you might be wondering how to bring those two together. In particular, how can we implement a state machine when we only receive and return logits in the logits processor.

The answer is that we extend logits processors to be stateful, which means they must be able to receive and return their own state.

We made a PR for adding state at to achieve right that:

After a first spike, the Bumblebee team (thank you!) suggested to create a new LogitsProcessor behaviour, as this will integrate well with Nx.

Welcome, Bumblebee.LogitsProcessor!

The design is similar to Bumblebee.Scheduler and involves two callbacks. Here is a stripped down version:

defmodule Bumblebee.LogitsProcessor do

  @callback init(t(), any()) :: state()

  @callback process(t(), state(), logits(), context()) :: {logits(), state()}

end

The first, init/2, must be used to create the initial state for each logit processor. As a result, all the initial states are known before the generation loop runs the first time. This is important for Nx to work with constant shapes.

The second, process/4 is doing the actual work. It's basically the same as the deftransform we've seen previously but instead of opts it receives a struct representing the logits processor, t(), and additionally the state.

Instead of returning only logits, it returns a tuple of logits and (modified) state. This way the logits processor can work with its state for multiple runs in the loop.

Implementing a DFA processor

Let's combine what we've learned so far and build a stateful logits processor!

We will make use of a DFA to ensure the generated output follows a schema.

First, we must implement both callbacks defined in Bumblebee.LogitsProcessor.

Let's start with init/2.

@callback init(t(), any()) :: state()

When we set up our DFA logits processor, we can pass it the definition of the DFA that describes the schema we want our generation to follow.

You can imagine this part as a struct, for the example given in Modeling schemas as DFA it would look like this.

%DFAProcessor{
  initial_state: 1,
  state_transitions: [
    {1, 1, 2},
    {2, 2, 3},
    {3, 3, 1}
  ]
}

We receive this struct as logits_processor as first argument in init/2.

Our goal in init/2 is to transform the data structures that define the DFA into tensors, so that we can work with them inside defn.

We can turn initial_state into a tensor by passing it to Nx.tensor/1.

initial_state =
  List.wrap(dfa.initial_state)
  |> Enum.map(&List.wrap(&1))
  |> Nx.tensor()

It's a bit more involved

Now we have the valid state transitions represented as list of tuples. What we want to build is basically a table where the rows represent the current state, the columns represent the token ID we select and the table entries represent the next state.

This would be the table for our example, e.g. if we are in state 1 (row 1) and select token ID 1 (column 1), we are going to move into state 2 (the value at row 1/column 1).

State/Token ID	1	2	3
1	2	0	0
2	0	3	0
3	0	0	1

We build this step by step as a tensor.

The grammar data format

We start by creating an empty tensor of the right dimensions, empty here means we fill it with 0s. When we look at the table, we can see which dimensions we need for the tensor. We need as many rows as we have states and as many columns as we have token IDs.

To simplify working with the tensor in Nx where dimensions always start at 0, we introduce an additional row 0 and column 0, so the table will look like this.

State/Token ID	0	1	2	3
0	0	0	0	0
1	0	2	0	0
2	0	0	3	0
3	0	0	0	1

Note that the number of token IDs is usually defined by the vocabulary size of the tokenizer we use.

So, this is how we create the empty tensor, we fill (Nx.broadcast/2) a tensor of size {num_states + 1, dfa.vocab_size} with 0.

num_states =
  dfa.state_transitions
  |> Enum.flat_map(fn {state, _token_id, next_state} -> [state, next_state] end)
  |> Enum.uniq()
  |> Enum.count()

empty_state_transitions_tensor = Nx.broadcast(0, {num_states + 1, dfa.vocab_size})

Next, we want to insert the state transitions into the empty tensor. We have to find the correct index. Remember, rows are states, columns are token IDs. Then, we set the value at this index to the next state according to our state transitions using Nx.indexed_put/3.

state_transitions_tensor =
  for transition <- dfa.state_transitions, reduce: empty_state_transitions_tensor do
    transitions_tensor ->
      {current_state, token_id, next_state} = transition
      index = Nx.tensor([current_state, token_id])

      Nx.indexed_put(transitions_tensor, index, next_state)
  end

The init callback

Now, we can return this state from init/2, a map containing initial_state and state_transitions_tensor.

%{
  dfa_state: %{
    last_state: initial_state,
    state_transitions_tensor: state_transition_tensors
  }
}

The process callback

Let's move on to implementing the second callback, process/4. We receive the configuration of the logit processor, t(), which we don't need in our case. Furthermore, we get state, logits, and context.

@callback process(t(), state(), logits(), context()) :: {logits(), state()}

First, we must find out in which state of our DFA we're currently in. Remember that whenever we enter process/4, we don't know which token was selected at the end of the last iteration of the loop.

However, we can retrieve the last_state we stored the previous time we ran the function and find the last_token_id at the end of context.sequence.

With these two pieces and our state_transitions_tensor, we can find the current_state.

The very first time we run process/4, we can just use the initial_state we have set in init/2. We can identify this situation by comparing two fields in the context: context.input_length is the length of the input (prompt), context.length is the complete length of input and generated response so far.

defnp current_state(context, last_state, transitions_tensor) do
  if context.length == context.input_length do
    last_state
  else
    last_token_id = context.sequence[context.length - 1]
    transitions_tensor[[Nx.squeeze(last_state), last_token_id]]
  end
end

With current_state on the other hand, we can determine which tokens we want to allow. Then, we can suppress the logits that are not allowed, by setting them to -infinity.

defnp only_allowed_logits(logits, transitions_tensor, current_state) do
  suppressed_logits = Nx.fill(logits, Nx.Constants.neg_infinity(), type: Nx.type(logits))
  allowed_token_ids = transitions_tensor[Nx.squeeze(current_state)]

  Nx.select(allowed_token_ids, logits, suppressed_logits)
end

Last, we store current_state as last_state for the next round.

  @impl Bumblebee.LogitsProcessor
  def process(_logits_processor, state, logits, context) do
    dfa_processing(logits, state, context)
  end

  deftransform dfa_processing(logits, state, context) do
    transitions_tensor = state.dfa_state.state_transitions_tensor

    last_state = state.dfa_state.last_state |> Nx.vectorize(:batch)
    current_state = current_state(context, last_state, transitions_tensor)
    logits = only_allowed_logits(logits, transitions_tensor, current_state)

    current_state = Nx.devectorize(current_state, keep_names: false)

    dfa_state = %{state.dfa_state | last_state: current_state}

    state = %{state | dfa_state: dfa_state}

    {logits, state}
  end

  defnp current_state(context, last_state, transitions_tensor) do
    if context.length == context.input_length do
      last_state
    else
      last_token_id = context.sequence[context.length - 1]
      transitions_tensor[[Nx.squeeze(last_state), last_token_id]]
    end
  end

  defnp only_allowed_logits(logits, transitions_tensor, current_state) do
    suppressed_logits = Nx.fill(logits, Nx.Constants.neg_infinity(), type: Nx.type(logits))
    allowed_token_ids = transitions_tensor[Nx.squeeze(current_state)]

    Nx.select(allowed_token_ids, logits, suppressed_logits)
  end

Exiting Generation

At one point of this generation loop we reach a state where the End of Text (EOT) token is allowed, and the loop can stop. - Or we run out of tokens.

If that happens, our processor simply stops and the format might still be invalid. If you must avoid this, your processor needs to be aware of the number of tokens left, and switch to a "safe end" state.

What we have achieved

We can now give programmatic guard rails the generation process of open source models. This is especially helpful when we have multiple smaller models that we use to perform specific tasks. We release the models from the task of complying to a grammar. This also means that our prompts can be much simpler as we don't need to include reward hacking and blackmail just to make the LLM realise the importance of the output format.

Next Steps

We have a number of PR's lined up to cover this feature. After that, we will look for a way to include a converter from JSON to our state transition table format. While working on the PR's and this blogpost, we used the Outlines Core Library, which is written in Rust.

Some grammars, however, can not be expressed in JSON Schema. Let's consider LLama3 function calling for a moment:

[get_user_info(user_id=7890, special='black')]<|eot_id|>

This, clearly is not designed to work with JSON. EBNF could provide an input schema for those grammars. Sean Moriarity shows this in his (EBNF library)[https://github.com/seanmor5/ebnf].

We might build those features eventually as they are needed in our projects or for fun. However, if you require functionality urgently, you can always get in touch, we love to hear from you :)

Why bitcrowd?

Elixir is an excellent choice for applications due to its scalability, fault tolerance, and concurrency model. Its lightweight processes and message-passing architecture make it ideal for orchestrating complex AI workflows efficiently. bitcrowd's first Elixir ML project dates back to 2020, and we have since then enabled various clients to build and scale their AI projects.

bitcrowd is an excellent choice if you need a scalable RAG system or a fully integrated AI pipeline. We help you build, optimize, and maintain it with a focus on reliability and performance.

Drop us a line via email if you want to build your next AI project with Elixir. Or book a call with us to discuss your project.